
| 第10回日本情報オリンピック 予選6 |
 |
|
2010年12月23日
情報オリンピック日本委員会
|
この問題では,場合の数を効率よく数えることが求められている. M, N の値は小さいが,高得点を得るにはプログラムの実行時間や使用メモリの丁寧な見積もりが必要である.
J, O, I が下の図のように並んだ部分を「良い JOI 」と呼ぶことにする.

解法1
最も単純な解法として,考えられるすべての「良い旗」を作りその個数を数える,という方法がある. 文字が決まっていないすべての場所に対して J, O, I のどれにするかを考えたものが旗の候補であり, それぞれついて「良い旗」の条件をみたすものを数えればよい. この方法では 3( ? の個数 ) 通りの候補を調べることになり, 小さなデータ以外では時間がかかりすぎてしまう.
解法1’
決まっている文字は入力の条件に従うが 「良い旗」ではない旗 (すなわち,J, O, I が適切に並んでいる箇所がどこにもない旗) を「悪い旗」とよぶ. 「良い旗」の個数と「悪い旗」の個数を合わせると 3( ? の個数 ) になるので, 「悪い旗」の個数から答えは簡単に計算できる. 以下では,「悪い旗」の個数を数えることにしよう.
解法 1 と同様であるが,各場所の文字を 1 つずつ順番にあてはめて試す,という方針を考える. 以下のような search 関数により「悪い旗」の個数を数えることができる.
search ( 現在の場所 ) {
if ( すべての場所に文字をあてはめた ) {
answer := answer + 1
return
} else {
if ( 現在の場所が ? ) {
現在の場所に J をあてはめる
if ( 「良い JOI 」が生じなかった ) {
search ( 次の場所 )
}
現在の場所に O をあてはめる
if ( 「良い JOI 」が生じなかった ) {
search ( 次の場所 )
}
現在の場所に I をあてはめる
if ( 「良い JOI 」が生じなかった ) {
search ( 次の場所 )
}
} else {
(現在の場所に指定された文字をあてはめる)
if ( 「良い JOI 」が生じなかった ) {
search ( 次の場所 )
}
}
}
}
1 つでも「良い JOI 」が作られた段階で「悪い旗」にはならないことがわかるので, 探索を打ち切って高速化することができる. しかしこの方法でも結局最大で 3( ? の個数 ) 通り,少なくとも答えの個数の旗を試すことになり, 小さなデータ以外を現実的な時間で解くことはできない.
解法2
解法 1' で生じている無駄をなくすことを考えよう. 上の行から下の行へ,同じ行内では左の列から右の列へ,という順番で文字をあてはめていくものとする. 下の図のような状況を考える.
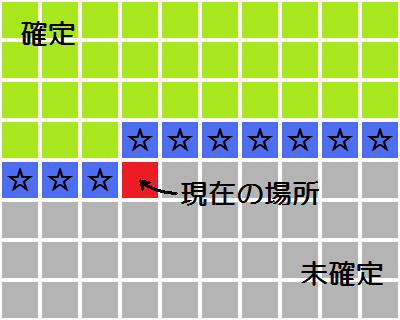
現在の場所以降に文字をあてはめていく過程において, 「良い JOI 」が生じたかどうかを判定するときに ☆で示した場所より上の部分にどのように文字をあてはめたかは全く関係ないことに注意する. このことにより,☆で示した場所 (現在の場所の直前 N 個) の文字が全く同じ状態にあったとき 「未確定」の場所に文字をあてはめていく作業を 2 回以上行うことが無駄であるのがわかる. よって,次の値が順次計算できることになる:
この解法での計算時間を見積もろう. 「現在の場所」は M * N 通りある. 「その直前 N 個の文字」は旗の外側の場所を文字 I として考えてよいことがわかるので,3N 通りある. 上の値はそれぞれ M, N に依らない時間で計算できるので,全体での計算時間は 3N * M * N となる. これは M, N が 10 程度であれば十分高速に計算できる (採点用データに対しては,半分前後の部分点を獲得できる) が, 320 * 20 * 20 > 1012 より,最大のデータに対してはやはり時間がかかりすぎてしまう.
注意
この問題では場合の数を 100000 で割った値を答えることに注意しなければならない. さらに,考えられる「良い旗」の個数は非常に大きな値になることがあるため, 「上の解法で個数を求めた後に,最後に 100000 で割って出力する」 という方法を用いるとオーバーフローが発生してしまう場合がある. そこで,上述の方法で (*) の値を求めていく際に,「 (*) の値を 100000 で割った余り」を代わりに求めていくようにすればよい.
解法3
メインアイデアは解法 2 で述べたものである. ☆で示した場所について,「隣り合う 2 つの文字が "JO" となっているか否か」のみが重要であるという点に着目する. 計算する値として,
を考えればよい. 「直前 1 個の文字が J であるか否か」は, 「現在の場所」の部分に新しく "JO" ができるかどうかを調べるために使われる.
この解法での計算時間は,「その直前 n 個の文字において隣り合う 2 列の文字がそれぞれ "JO" となっているか否か」 が 2N-1 通りであるから,全体で 2N * M * N となる. 220 * 20 * 20 ≒ 4 × 108 であり, うまくプログラムを組めば最大のデータでも数十秒以内に答えを求めることができる.
参考
解法 3 の計算時間をより丁寧に分析する. 「その直前 N 個の文字において隣り合う 2 列の文字がそれぞれ "JO" となっているか否か」 について, 「 a 列目と a+1 列目が "JO" となっていて, a+1 列目と a+2 列目が "JO" になっている」 ということは起こり得ない. すると,「○と×を,○が隣り合わないように N-1 個並べる場合の数」を考えればよいが, これはフィボナッチ数で表されることが知られている. N = 20 に対してはこれは 10946 通りしかなく,このことを利用するとさらに効率よく計算することができる.